The Material Point Method (MPM), which is an extension of the particle-in-cell method , provides a promising numerical framework which can naturally handle classical problems involving severe deformations, such as landslides. Interested readers may refer to a general introduction by Fern et al. about MPM here. We are currently developing an MPM matlab solver capable of solving a variety of elastoplastic problems, ranging from granular impacts to granular collapse.
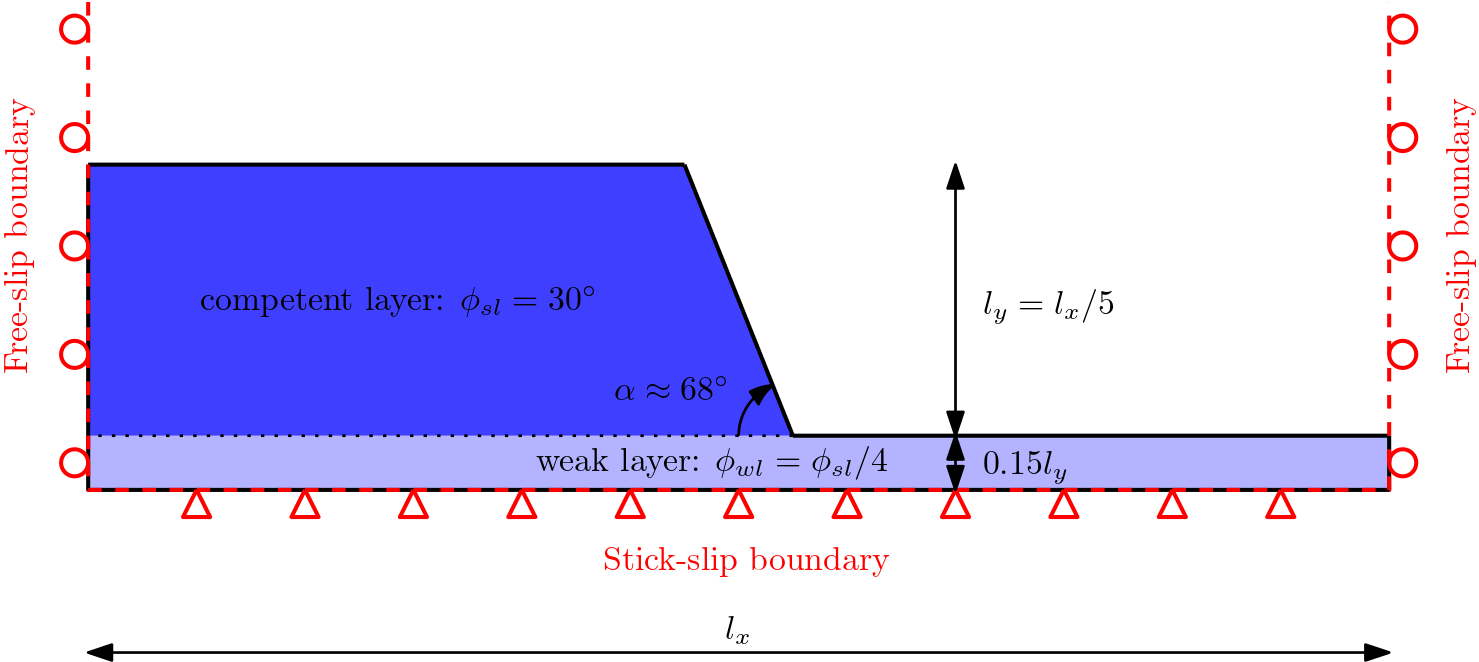
We here only intend to show some preliminary results of a typical slumping process governed by a Coulomb type material with a non-associated flow rule, considering i) a weak layer with a lower internal frictional angle, (ii) an heterogeneous cohesion field and, iii) a strain weakening behavior of the material.
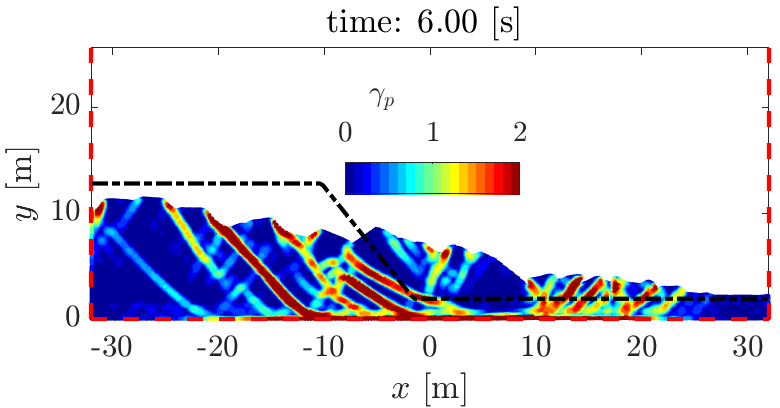
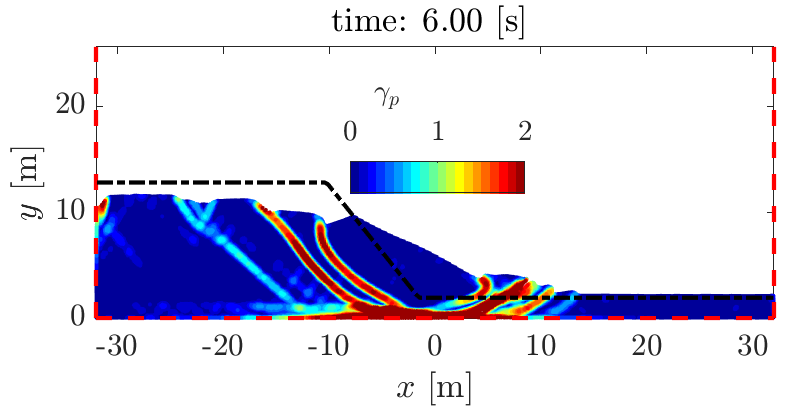
The initial geometry of the problem is described in the Figure below. We can set different value for the basal friction, i.e., mu is ranging from 0 (free slip boundary) to 0.5 (increasing stick-slip behavior at the interface). The mass instantly deforms under self-weight loading, i.e., the solver does not iterate to converge toward a force equilibrium before plastic loading to occur.
The two following numerical solution after 6 seconds shows naturally an important contribution of the basal friction both on the strain localization and the runout distance of the slumping mass. This also suggest different modes of deformation regarding the frictional behavior at the basal interface.
Deeper investigations are now required to fully understand the complex nonlinear behavior of a slumping mass.