
Grégoire Mariéthoz s’intéresse à différents processus environnementaux liés à l’hydrologie et au climat:
Comment déterminer la couverture neigeuse sur la base d’images satellites ? Comment les régimes de précipitations vont-ils évoluer avec le changement climatique ? Quelle sera l’influence du changement climatique sur la végétation alpine ?, etc.
Pour comprendre ces processus naturels et leur évolution, Grégoire Mariéthoz utilise des modèles stochastiques qui traduisent les variabilités spatiales et temporelles de ces systèmes. Les données liées aux paramètres étudiés font partie des éléments-clés pour pouvoir développer ces modèles. Bien qu’on observe actuellement un afflux de données numériques provenant de multiples systèmes de capteurs, celles-ci ne sont pas toujours en nombre suffisant pour étudier certains paramètres ou zones spécifiques (nombre de capteurs limité, mesures très ponctuelles, événements rares etc.). Grégoire Mariéthoz et son équipe développent des méthodes statistiques qui visent à combler ces lacunes et à optimiser l’information issue des données à disposition.
Procéder de proche en proche pour remplir les vides
Ces méthodes présentent un intérêt notamment dans l’étude des processus à petite échelle temporelle ou géographique. Ces approches sont importantes, sachant que les phénomènes climatiques les plus violents se produisent généralement dans des zones très ciblées et peuvent occasionner localement beaucoup de dégâts (tornades, orages violents, trombes d’eau etc). Ces événements sont actuellement difficiles à prévoir et tendent à devenir plus fréquents avec le changement climatique. Le challenge auquel est confronté Grégoire Mariéthoz face à ces questions est d’arriver à identifier des schémas cohérents à partir de données très fragmentaires et de processus parfois aléatoires.
Pour y parvenir, ce dernier développe des outils qui permettent de déduire la valeur d‘un paramètre situé près d’une mesure directe, en s’appuyant sur des lois physiques et diverses méthodes statistiques. En procédant ainsi de proche en proche, il lui est possible de combler des intervalles manquants entre deux mesures et d’obtenir des sets de données complets. Grégoire Mariéthoz a pu ainsi modéliser des historiques de pluviométrie, reconstituer des images tronquées, ou recréer l’historique de la couverture neigeuse dans les alpes (cf encadré).
L’utilisation de l’IA progresse, mais ne remplace pas tous les modèles
Si l’IA et ses algorithmes existent depuis longtemps déjà, Grégoire Mariéthoz la voit se développer maintenant grâce entre autres, à l’avalanche massive de données exploitables, à la densification de divers capteurs (satellites, radars, webcams) et à la mise à disposition de ces données en open source. La disponibilité d’ordinateurs de plus en plus performants joue aussi un rôle. L’IA fournit ainsi des outils intéressants (comme ChatGPT ou les générateurs d’images), mais elle ne répond pas à toutes les situations et ne peut pas créer de nouvelles connaissances. Selon lui un modèle basé sur l’IA n’est pas forcément meilleur qu’un autre : « Si l’on veut modéliser un événement ou un phénomène précis, les modèles classiques peuvent souvent être implémentés en tenant compte de la connaissance des processus. En revanche, lorsque beaucoup de données sont disponibles, il peut devenir intéressant d’intégrer l’IA et de consacrer du temps à récolter la masse de données nécessaire et à entraîner l’ordinateur. Cette balance d’investissement de temps est l’un des critères déterminants pour le choix d’utilisation de l’IA.»
Déterminer l’évolution de la couche neigeuse au cours du temps à partir d’images satellites actuelles
Grégoire Mariéthoz et ses collègues ont pour objectif de modéliser l’évolution de la couverture neigeuse en Suisse, notamment car celle-ci représente un très bon indicateur des variations de température et de climat, et peut impacter fortement l’hydrologie locale lors de sa fonte. La quantité de neige couvrant une zone donnée peut être observée soit directement, par des mesures au sol et des stations météo, soit indirectement, via des images satellites. Ces images sont parfois difficiles à interpréter : des zones à l’ombre peuvent être considérées comme sans neige car plus sombres (actuellement certains satellites fournissent des données plus fiables grâce à l’ajout de mesure de rayonnement infrarouge notamment), ou la vision du sol est perturbée par la présence d’une couche nuageuse. A cela s’ajoute le rythme des prises de vue qui est irrégulier, (tous les 3 à 5 jours), ce qui rend imparfaitement compte d’un phénomène pouvant évoluer d’un jour à l’autre.
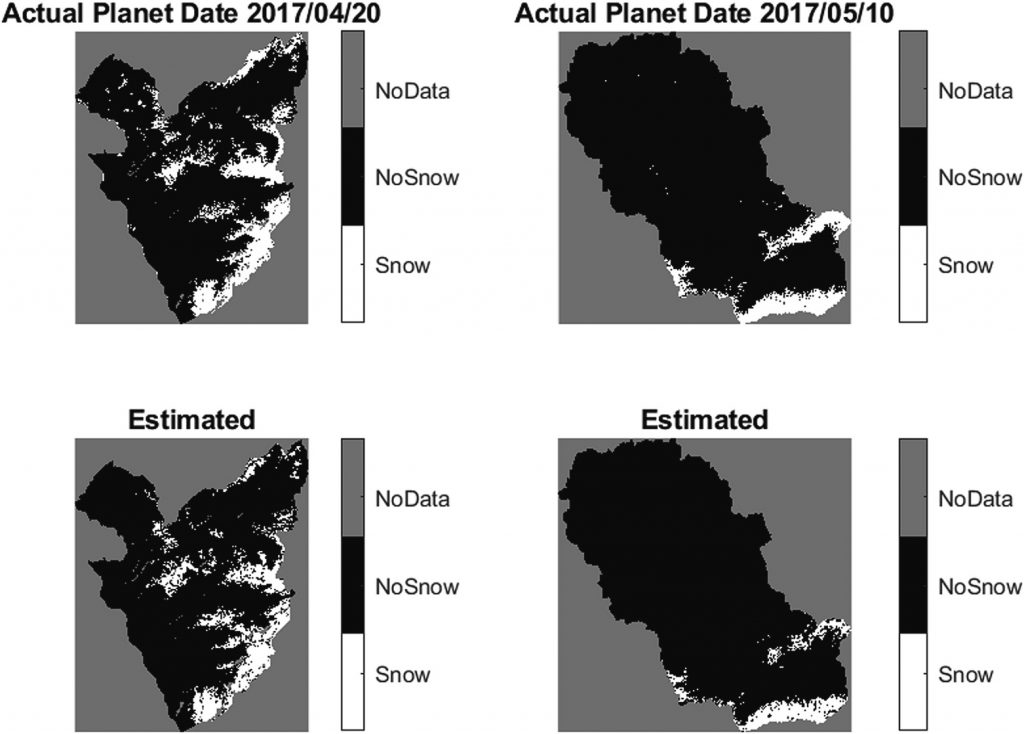
Pour contourner ce problème, Grégoire Mariéthoz s’est basé sur le principe que l’évolution de la couverture neigeuse suit des schémas constants d’une année à l’autre, lorsque les conditions météo sont similaires. Il a développé des algorithmes apprenant à l’ordinateur à relier les valeurs de températures et de précipitations mesurées au sol, à la couverture neigeuses observée sur des images satellites interprétables sans ambiguïté (en incluant également d’autres paramètres géomorphologiques comme la topographie et l’exposition). En reprenant les données climatiques de différentes périodes, il lui a ainsi été possible de créer des images satellites “synthétiques“ de la couverture neigeuse des régions observées. Les projections effectuées ont pu être validées, d’une part avec une comparaison par rapport à des mesures faites sur site, et d’autre part avec des images prises par un autre satellite. Dans tous les cas, les images synthétiques prédisent une répartition de la couverture neigeuse plus proche de la réalité que celle des modèles traditionnels qui se basent uniquement sur les processus physiques de fonte de la neige.
Pour aller plus loin
Modèle stochastique : Un modèle stochastique est un modèle mathématique qui prend en compte l’incertitude ou le caractère aléatoire de certains des paramètres étudiés. Contrairement aux modèles déterministes qui produisent des résultats identiques pour des conditions initiales données, les modèles stochastiques intègrent des éléments de hasard dans leurs formulations. Ces modèles sont souvent utilisés pour représenter des phénomènes influencés par des variables aléatoires ou des processus aléatoires.
Dans un modèle stochastique, les résultats ne sont pas prédéterminés, mais sont plutôt caractérisés par des distributions de probabilité. Cela permet de mieux représenter des phénomènes réels qui peuvent être soumis à des variations imprévisibles ou à des fluctuations aléatoires. Les modèles stochastiques sont couramment utilisés dans divers domaines tels que la finance, la météorologie, la physique des particules, et d’autres domaines où l’incertitude et le hasard jouent un rôle significatif.
Laisser un commentaire